LeetCode Problems: Linked List
Linked List in Leetcode
Summary
-
Main types:
- Singly Linked List

- Doubly Linked List

- Circular Linked List (can be used to solve Josephus problem)

- Doubly Linked List
- Singly Linked List
-
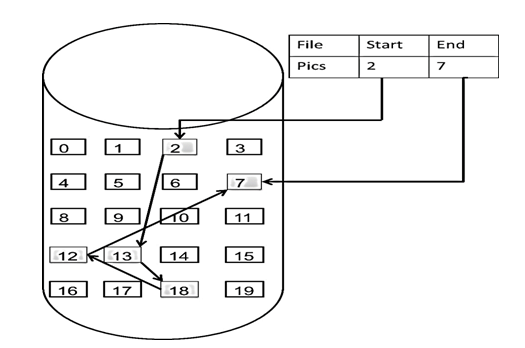
How is linked list stored in memory?
- It is stored at non-contiguous locations in memory (nodes), connected by links. Each node contains data and a pointer to the next node.
Type of Questions:
Using Dummy Head Node
- One of the major problems with linked lists is that to handle the current node, you have to find the previous node. It makes it difficult to deal with the head node since it does not have a previous node.
- Every time you handle the head node, you have to do it separately. So, using the dummy head node trick can solve this problem.
- 203. Remove Linked List Elements
- Singly-linked list remove elements
- My solution: Adding a dummy node before the head node, dropping it when returning the solution.
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:
if head == None: return head
nh = ListNode(next=head)
prev = nh
curr = head
while curr:
if curr.val == val:
prev.next = curr.next
else: prev = curr
curr = curr.next
return nh.next
Linked List Basic Operations
- 707. Design Linked List
- Design your implementation of the linked list.
class Node:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
class MyLinkedList:
def __init__(self):
self.head = None
self.tail = None
self.length = 0
def get(self, index: int) -> int:
if index >= self.length: return -1
curr = self.head
for _ in range(index):
curr = curr.next
return curr.val
def addAtHead(self, val: int) -> None:
nh = Node(val)
if self.length == 0:
self.head = nh
self.tail = nh
self.length += 1
return
nh.next = self.head
self.head = nh
self.length += 1
# print(self.printList(self.head))
def addAtTail(self, val: int) -> None:
nt = Node(val)
if self.length == 0:
self.head = nt
self.tail = nt
self.length += 1
return
self.tail.next = nt
self.tail = nt
self.length += 1
# print(self.printList(self.head))
def addAtIndex(self, index: int, val: int) -> None:
if index > self.length: return
if index == 0:
self.addAtHead(val)
return
if index == self.length:
self.addAtTail(val)
return
nn = Node(val)
curr = self.head
for _ in range(index - 1):
curr = curr.next
nn.next = curr.next
curr.next = nn
self.length += 1
# print(self.printList(self.head))
def deleteAtIndex(self, index: int) -> None:
if index >= self.length: return
if index == 0:
self.head = self.head.next
self.length -= 1
return
curr = self.head
for _ in range(index - 1):
curr = curr.next
if curr.next == self.tail:
self.tail = curr
curr.next = curr.next.next
self.length -= 1
# print(self.printList(self.head))
# printing the linked list, only for debug
# def printList(self, head) -> str:
# curr = head
# res = ""
# while curr:
# res = res + " " + str(curr.val)
# curr = curr.next
# return res
Reverse Linked List
- Reverse a linked list iteratively or recursively.
- 206. Reverse Linked List
- Given the head of a singly linked list, reverse the list, and return the reversed list.
- Nothing special, just keep flipping the arrows
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
prev, curr = None, head
while curr:
nxt = curr.next
curr.next = prev
prev = curr
curr = nxt
return prev
class Solution: # Recursive method: similar to two pointers, the idea is also flipping the arrows
def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
# make sure you declare the helper function inside the class
def reverse(prev, curr):
if (curr == None): return prev
nxt = curr.next
curr.next = prev
return reverse(curr, nxt)
return reverse(None, head)
Swap Nodes in Pairs
- 24. Swap Nodes in Pairs
- Given a linked list, swap every two adjacent nodes and return its head. You must solve the problem without modifying the values in the list's nodes (i.e., only nodes themselves may be changed.)
-
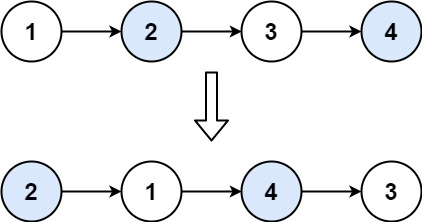
- p is traversing the linked list 2 steps at a time, last_pair keeps track of the last node of the last pair so that we can update its next pointer when the next pair is reversed.
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:
if head == None: return head
if head.next == None: return head
last_pair = None
nh = head.next
p = head
while p:
q = p.next
if q == None: break
nxt = q.next
q.next = p
p.next = nxt
if last_pair:
last_pair.next = q
last_pair = p
p = nxt
return nh
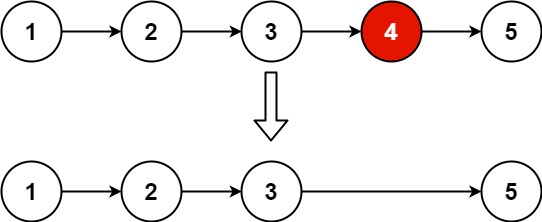
Remove Nth Node From End of List
- 19. Remove Nth Node From End of List
- My solution: Calculate the index of node to delete -- Still O(n)
- Other solution: Dummy Head Node + Fast & Slow Pointers (See Solution 2). To delete the N-th last node, first move the fast pointer n + 1 steps (so that when we move fast and slow pointers together, the slow pointer points to the last node of the node to delete), then move fast and slow pointers at the same time until the fast pointer reaches the end. Finally, delete the next node of the slow pointer.
-
class Solution1:
def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
length = 0
curr = head
while curr:
length += 1
curr = curr.next
idx = length - n
if idx == 0:
return head.next
curr = head
for _ in range(idx - 1):
curr = curr.next
curr.next = curr.next.next
return head
class Solution2:
def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
nn = ListNode(next=head)
s = f = nn
for _ in range(n + 1):
f = f.next
while f:
s = s.next
f = f.next
s.next = s.next.next
return nn.next
Intersection of Two Linked Lists
- 160. Intersection of Two Linked Lists
- Given the heads of two singly linked-lists headA and headB, return the node at which the two lists intersect. If the two linked lists have no intersection at all, return null.
- My solution: Get the length of each linked list first, then align the end of two linked lists. Move the pointers pa and pb simultaneously until the end to see if there is an intersection.
-

class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:
# get the length of each linked list first
la = lb = 0
curr = headA
while curr:
la += 1
curr = curr.next
curr = headB
while curr:
lb += 1
curr = curr.next
# align the end of two linked lists
start = abs(la - lb)
pa, pb = headA, headB
if la > lb:
for _ in range(start):
pa = pa.next
else:
for _ in range(start):
pb = pb.next
while pa and pb:
if pa == pb:
return pa
pa = pa.next
pb = pb.next
return None
Linked List Cycle II
- Find cycle and the start of the cycle.
- This type of question is arguably one of the most difficult ones for linked lists. However, the code is clear and simple. The hard part is the mathematical patterns and proofs.
- 142. Linked List Cycle II
- Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.
- My solution (using O(n) memory): Keep an array of visited nodes. If the node is in the visited node array, return the node (must be the start of the cycle).
-
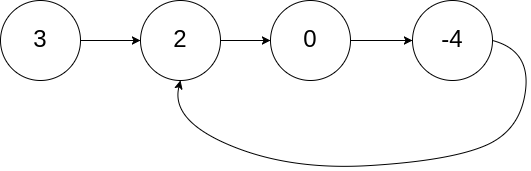
- Solution using O(1) memory (Fast & Slow Pointers):
- Detect cycle using fast (2 steps per move) & slow (1 step per move) pointers. If there is a cycle, fast and slow pointers will meet inside the cycle.
- Find the starting node of the cycle.
-
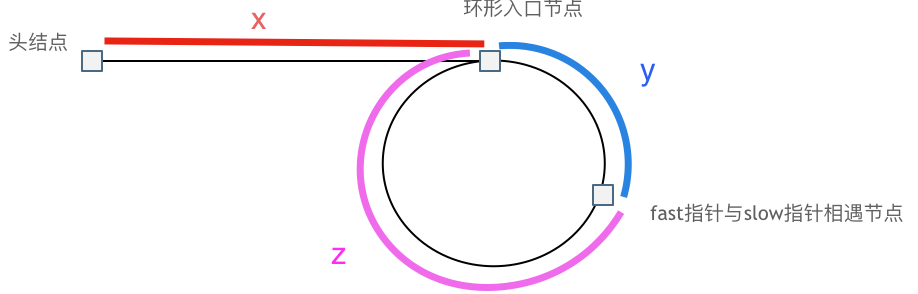
- When fast and slow pointers meet, the slow pointer passes x + y nodes, and the fast pointer passes $$x + y + n * (y + z)$$ where n is the number of loops the fast pointer has passed in the cycle. The number of nodes the fast pointer has passed is twice the one of the slow pointer, i.e., 2 * (x + y). Therefore, $$x + y = n * (y + z)$$ $$=> x = n * (y + z) - y = (n - 1)(y + z) + z$$
- When n = 1, x = z. We can then use two pointers, one starting from the head of the linked list and the other starting from the meeting node. When these two pointers meet, we find the start of the cycle.
-
-
class Solution: # O(n) space complexity
def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
visited = []
curr = head
while curr:
if curr in visited:
return curr
visited.append(curr)
curr = curr.next
return None
class Solution: # O(1) space complexity
def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
s = f = head
# checking f.next since f is moving 2 steps at a time
while f and f.next:
s = s.next
f = f.next.next
if s == f:
i1, i2 = head, s
while i1 != i2:
i1 = i1.next
i2 = i2.next
return i1
return None
Credit: Programmer Carl LeetCode Master
