July LeetCoding Challenge 2022
Notes for ☀️ July LeetCoding Challenge 🗓 questions. Practice makes a man perfect loll :)
Day 1
- 1710. Maximum Units on a Truck
- My solution: sort the array by number of units per box in descending order, then loop on the array and put boxes onto one truck greedily.
class Solution:
def maximumUnits(self, b: List[List[int]], t: int) -> int:
def getSecond(elmt):
return elmt[1]
b.sort(key=getSecond, reverse=True)
res = 0
for i in range(len(b)):
if t <= 0:
break
nb, nupb = b[i][0], b[i][1]
if t < nb:
res += t * nupb
break
res += nb * nupb
t -= nb
return res
Day 2
- 1465. Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts
- You are given a rectangular cake of size h x w and two arrays of integers horizontalCuts and verticalCuts.
- Return the maximum area of a piece of cake after you cut at each horizontal and vertical position provided in the arrays horizontalCuts and verticalCuts. Since the answer can be a large number, return this modulo 10^9 + 7.
-
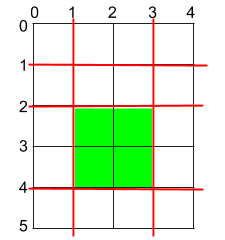
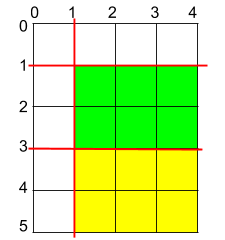
- My solution: Greedily find the maximum horizontal and vertical gaps, and the intersection of the gaps has the maximum area. Since we're dealing with rectangular, this property will hold (try it with your own cuts; you will see it's always true).
- You are given a rectangular cake of size h x w and two arrays of integers horizontalCuts and verticalCuts.
class Solution:
def maxArea(self, h: int, w: int,
hc: List[int],
vc: List[int]) -> int:
# find the max gap in a row/column
# l is the length of the row/column
# arr is the horizontal/vertical cuts
def findMaxGap(l, arr):
max_gap = max(arr[0], l - arr[-1])
for i in range(1, len(arr)):
max_gap = max(max_gap, arr[i] - arr[i-1])
return max_gap
# the arrays may not be sorted
hc.sort()
vc.sort()
h_max_gap = findMaxGap(h, hc)
v_max_gap = findMaxGap(w, vc)
# print(h_max_gap, v_max_gap)
# take modulo 10^9 + 7
return (h_max_gap * v_max_gap) % (10**9 + 7)
Day 5
- 128. Longest Consecutive Sequence
- Given an unsorted array of integers nums, return the length of the longest consecutive elements sequence.
- You must write an algorithm that runs in O(n) time.
class Solution: # My solution (O(nlogn) using sorting)
def longestConsecutive(self, nums: List[int]) -> int:
if nums == []: return 0
h = {}
for i in range(len(nums)):
h[nums[i]] = 1
cur = res = 0
for k in sorted(h.keys()):
if (k-1) in h:
cur += 1
else:
res = max(res, cur)
cur = 0
res = max(res, cur)
return res + 1
class Solution: # Optimal solution (O(n) hashSet and
# intelligent sequence building, the numbers
# are stored in a hashset/set (in python) to allow O(1) lookups)
def longestConsecutive(self, nums: List[int]) -> int:
res = 0
ns = set(nums)
for n in ns:
if n - 1 not in ns:
cn = n
cur = 1
while cn + 1 in ns:
cn += 1
cur += 1
res = max(res, cur)
return res
Day 6
- 509. Fibonacci Number
- The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence. Given n, calculate F(n).
- My solutions (basic dynamic programming or recursion):
class Solution: # Dynamic Programming
def fib(self, n: int) -> int:
if n == 0: return 0
if n == 1: return 1
f1, f2 = 0, 1
res = 0
while n > 1:
res = f1 + f2
f1 = f2
f2 = res
n -= 1
return res
class Solution: # recursion, notice it's self.fib
# instead of just fib when calling the function
def fib(self, n: int) -> int:
if n == 0: return 0
if n == 1: return 1
return self.fib(n - 2) + self.fib(n - 1)
Day 7
- 97. Interleaving String
- Given strings s1, s2, and s3, find whether s3 is formed by an interleaving of s1 and s2.
- An interleaving of two strings s and t is a configuration where they are divided into non-empty substrings such that:
- s = s1 + s2 + ... + sn
- t = t1 + t2 + ... + tm
- |n - m| <= 1
- The interleaving is s1 + t1 + s2 + t2 + s3 + t3 + ... or t1 + s1 + t2 + s2 + t3 + s3 + ...
-
- Approach 1: Brute Force (Time limit exceed)
- The most basic idea is to find every string possible by all interleavings of the two given strings s1 and s2. In order to implement this method, we are using recursion. We start by taking the current character of the first string s1 and then appending all possible interleavings of the remaining portion of the first string s1 and the second string s2 and comparing each result formed with the required interleaved string s3. Similarly, we choose one character from the second string s2 and form all the interleavings with the remaining portion of s2 and s1 to check if the required string s3 can be formed.
class Solution:
def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
def helper(s1, i, s2, j, res, s3):
if res == s3 and i == len(s1) and j == len(s2):
return True
ans = False
if i < len(s1):
ans = ans or helper(s1, i + 1, s2, j, res + s1[i], s3)
if j < len(s2):
ans = ans or helper(s1, i, s2, j + 1, res + s2[j], s3)
return ans
if len(s1) + len(s2) != len(s3): return False
return helper(s1, 0, s2, 0, "", s3)
- Approach 2: Recursion with memorization
- In the recursive approach discussed above, we are considering every possible string formed by interleaving the two given strings. But, there will be cases encountered in which, the same portion of s1 and s2 would have been processed already but in different orders(permutations). But irrespective of the order of processing, if the resultant string formed till now is matching with the required string(s3), the final result is dependent only on the remaining portions of s1 and s2, but not on the already processed portion. Thus, the recursive approach leads to redundant computations.
- This redundancy can be removed by making use of memoization along with recursion. For this, we maintain 3 pointers i, j, k which correspond to the index of the current character of s1, s2, s3 respectively. Also, we maintain a 2D memo array to keep a track of the substrings processed so far. memo[i][j] stores a 1/0 or -1 depending on whether the current portion of strings i.e. up to i-th index for s1 and up to j-th index for s2 has already been evaluated. Again, we start by selecting the current character of s1 (pointed by i). If it matches the current character of s3 (pointed by k), we include it in the processed string and call the same function recursively as: is_Interleave(s1, i+1, s2, j, s3, k+1, memo)
- Any time we find a match in our memo table it implies we've tried interleaving as far as possible without finding an answer, so we can return false right away.
class Solution:
def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
if len(s1) + len(s2) != len(s3):
return False
def helper(i, j, k):
if (i, j) in seen:
return False
seen.add((i, j))
if i == len(s1):
return s2[j:] == s3[k:]
if j == len(s2):
return s1[i:] == s3[k:]
if ((s1[i] == s3[k] and helper(i + 1, j, k + 1)) or
(s2[j] == s3[k] and helper(i, j + 1, k + 1))):
return True
return False
seen = set()
return helper(0, 0, 0)
- Approach 3: Using 2D Dynamic Programming
- The recursive approach discussed in above solution included a character from one of the strings s1 or s2 in the resultant interleaved string and called a recursive function to check whether the remaining portions of s1 and s2 can be interleaved to form the remaining portion of s3. In the current approach, we look at the same problem the other way around. Here, we include one character from s1 or s2 and check whether the resultant string formed so far by one particular interleaving of the the current prefix of s1 and s2 form a prefix of s3.
- Thus, this approach relies on the fact that the in order to determine whether a substring of s3(upto index k), can be formed by interleaving strings s1 and s2 upto indices i and j respectively, solely depends on the characters of s1 and s2 upto indices i and j only and not on the characters coming afterwards.
class Solution:
def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
if len(s1) + len(s2) != len(s3):
return False
dp = [[0 for _ in range(len(s1)+1)] for _ in range(len(s2)+1)]
for i in range(len(s1)):
for j in range(len(s2)):
if i == 0 and j == 0:
dp[i][j] = True
elif i == 0:
dp[i][j] = dp[i][j-1] and s2[j-1] == s3[i+j-1]
elif j = 0:
dp[i][j] = dp[i-1][j] and s1[i-1] == s3[i+j-1]
else:
dp[i][j] = (dp[i-1][j] and s1[i-1] == s3[i+j-1]) or (dp[i][j-1] and s2[j-1] == s3[i+j-1])
return dp[len(s1)][len(s2)]
- Approach 4: Using 1D Dynamic Programming
- This approach is the same as the previous approach except that we have used only 1D dp array to store the results of the prefixes of the strings processed so far. Instead of maintaining a 2D array, we can maintain a 1D array only and update the array's element dp[i] when needed using dp[i-1] and the previous value of dp[i].
class Solution:
def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
if len(s1) + len(s2) != len(s3):
return False
dp = [0 for _ in range(len(s2)+1)]
for i in range(len(s1)):
for j in range(len(s2)):
if i == 0 and j == 0:
dp[j] = True
elif i == 0:
dp[j] = dp[j-1] and s2[j-1] == s3[i+j-1]
elif j = 0:
dp[j] = dp[j] and s1[i-1] == s3[i+j-1]
else:
dp[j] = (dp[j] and s1[i-1] == s3[i+j-1]) or (dp[j-1] and s2[j-1] == s3[i+j-1])
return dp[len(s2)]
Day 10
- 746. Min Cost Climbing Stairs
- You are given an integer array cost where cost[i] is the cost of ith step on a staircase. Once you pay the cost, you can either climb one or two steps.
- You can either start from the step with index 0, or the step with index 1.
- Return the minimum cost to reach the top of the floor.
class Solution: # just DP
def minCostClimbingStairs(self, cost: List[int]) -> int:
if len(cost) == 2: return min(cost[0], cost[1])
dp = [0 for _ in range(len(cost))]
dp[0] = cost[0]
dp[1] = cost[1]
for i in range(2, len(cost)):
if i == len(cost) - 1:
dp[i] = min(dp[i - 1], dp[i - 2] + cost[i])
else:
dp[i] = min(cost[i] + dp[i - 2], dp[i - 1] + cost[i])
return dp[len(cost) - 1]
Day 11
- 199. Binary Tree Right Side View
- Given the root of a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution: # Using queue to traverse each level of the tree
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
if root == None: return []
q = [root]
res = []
while q:
size = len(q)
n = size
while n:
n -= 1
node = q.pop(0)
if n == 0:
res.append(node.val)
if node.left: q.append(node.left)
if node.right: q.append(node.right)
return res
class Solution: # or we update the length of next level while traversing
# to eliminate the len(q) overhead at each level.
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
if root == None: return []
q = [root]
res = []
curSize = 1
while q:
nxtSize = 0
for i in range(curSize):
node = q.pop(0)
if i == curSize - 1:
res.append(node.val)
if node.left:
q.append(node.left)
nxtSize += 1
if node.right:
q.append(node.right)
nxtSize += 1
curSize = nxtSize
return res
Day 12 (Failed to solve it at the first time)
- 473. Matchsticks to Square
- You are given an integer array matchsticks where matchsticks[i] is the length of the i-th matchstick. You want to use all the matchsticks to make one square. You should not break any stick, but you can link them up, and each matchstick must be used exactly one time.
- Return true if you can make this square and false otherwise.
-
- Similar question: 698
class Solution: # DFS
def makesquare(self, nums: List[int]) -> bool:
# If there are no matchsticks, then we can't form any square
if not nums:
return False
# Number of matchsticks we have
L = len(nums)
# Perimeter of our square (if one can be formed)
perimeter = sum(nums)
# If the perimeter can be equally split into 4 parts (and hence 4 sides, then we move on).
if perimeter % 4 != 0:
return False
# Side of our square.
side = perimeter / 4
# Reverse sort the matchsticks because we want to consider the biggest one first.
nums.sort(reverse=True)
# This array represents the 4 sides and their current lengths
sums = [0 for _ in range(4)]
# Our recursive dfs function.
def dfs(index):
# If we reach the end of matchsticks array, we check if the square was formed or not
if index == L:
# If 3 equal sides were formed, 4th will be the same as these three and answer should be True in that case.
return sums[0] == sums[1] == sums[2] == side
# The current matchstick can belong to any of the 4 sides (provided their remaining lenghts are >= the size of the current matchstick)
for i in range(4):
# If this matchstick can fit in the space left for the current side
if sums[i] + nums[index] <= side:
# Recurse
sums[i] += nums[index]
if dfs(index + 1):
return True
# Revert the effects of recursion because we no longer need them for other recursions.
sums[i] -= nums[index]
return False
return dfs(0)
class Solution:
def makesquare(self, nums: List[int]) -> bool:
# If there are no matchsticks, then we can't form any square.
if not nums:
return False
# Number of matchsticks
L = len(nums)
# Possible perimeter of our square
perimeter = sum(nums)
# Possible side of our square from the given matchsticks
possible_side = perimeter // 4
# If the perimeter isn't equally divisible among 4 sides, return False.
if possible_side * 4 != perimeter:
return False
# Memoization cache for the dynamic programming solution.
memo = {}
# mask and the sides_done define the state of our recursion.
def recurse(mask, sides_done):
# This will calculate the total sum of matchsticks used till now using the bits of the mask.
total = 0
for i in range(L - 1, -1, -1):
if not (mask & (1 << i)):
total += nums[L - 1 - i]
# If some of the matchsticks have been used and the sum is divisible by our square's side, then we increment the number of sides completed.
if total > 0 and total % possible_side == 0:
sides_done += 1
# If we were successfully able to form 3 sides, return True
if sides_done == 3:
return True
# If this recursion state has already been calculated, just return the stored value.
if (mask, sides_done) in memo:
return memo[(mask, sides_done)]
# Common variable to store answer from all possible further recursions from this step.
ans = False
# rem stores available space in the current side (incomplete).
c = int(total / possible_side)
rem = possible_side * (c + 1) - total
# Iterate over all the matchsticks
for i in range(L - 1, -1, -1):
# If the current one can fit in the remaining space of the side and it hasn't already been taken, then try it out
if nums[L - 1 - i] <= rem and mask&(1 << i):
# If the recursion after considering this matchstick gives a True result, just break. No need to look any further.
# mask ^ (1 << i) makes the i^th from the right, 0 making it unavailable in future recursions.
if recurse(mask ^ (1 << i), sides_done):
ans = True
break
# cache the result for the current recursion state.
memo[(mask, sides_done)] = ans
return ans
# recurse with the initial mask with all matchsticks available.
return recurse((1 << L) - 1, 0)
Day 13
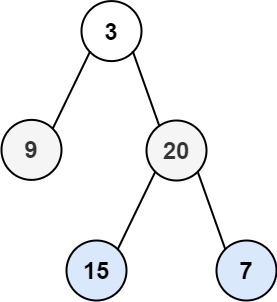
- 102. Binary Tree Level Order Traversal
- Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).
-
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if root == None: return []
q = [root]
res = []
while q:
size = len(q)
n = size
curr = []
# print(q)
while n:
node = q.pop(0)
curr.append(node.val)
if node.left: q.append(node.left)
if node.right: q.append(node.right)
n -= 1
res.append(curr)
return res
Day 14 (Failed to solve at the first time)
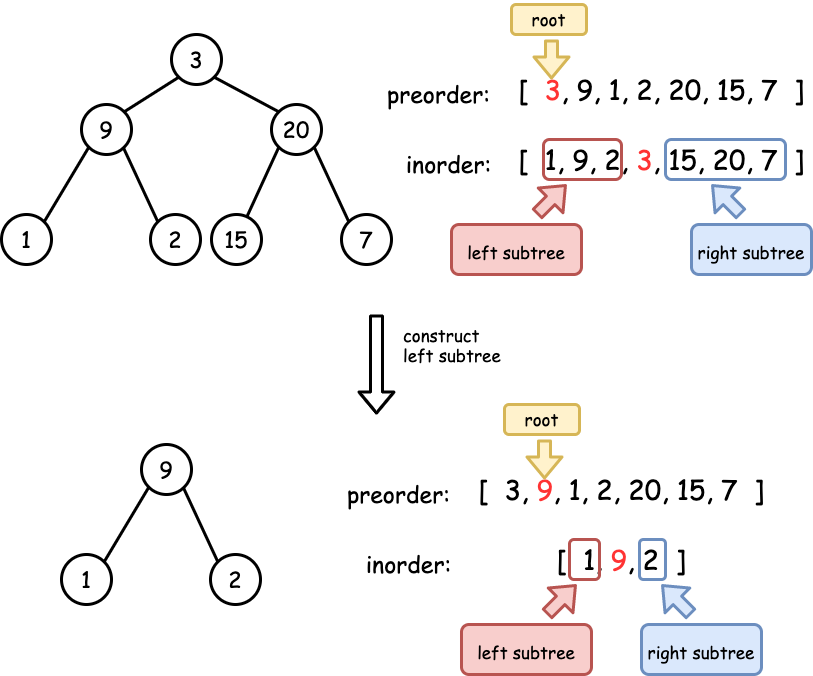
- 105. Construct Binary Tree from Preorder and Inorder Traversal
- Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.
-
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
if inorder:
idx = inorder.index(preorder.pop(0))
root = TreeNode(inorder[idx])
root.left = self.buildTree(preorder, inorder[:idx])
root.right = self.buildTree(preorder, inorder[idx+1:])
return root
Day 15 (Failed to solve at the first time)
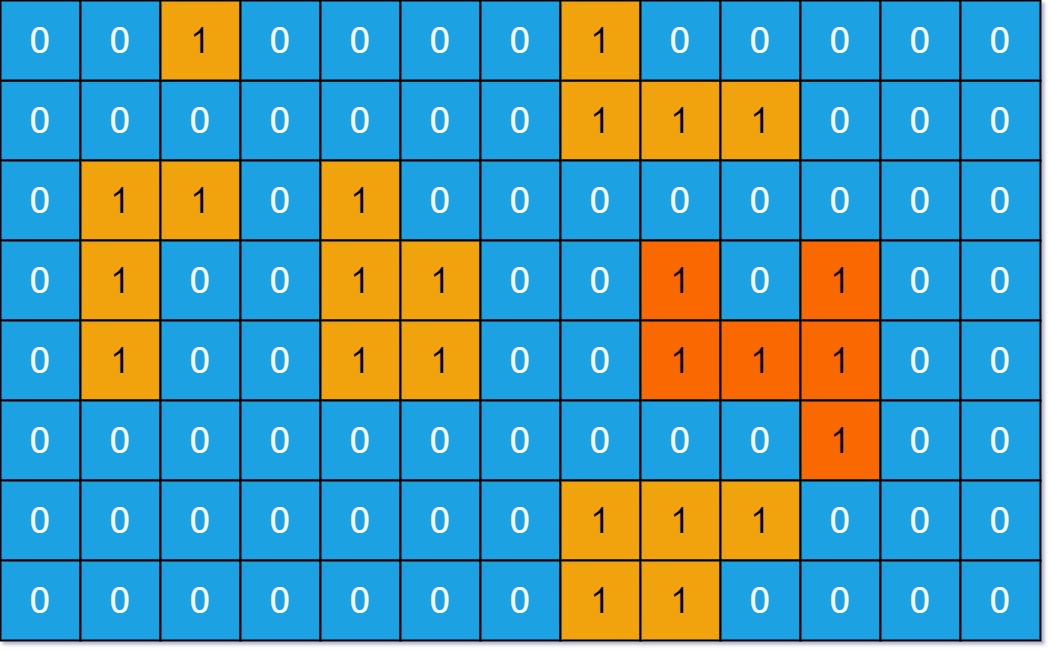
- 695. Max Area of Island
- You are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.
- The area of an island is the number of cells with a value 1 in the island.
- Return the maximum area of an island in grid. If there is no island, return 0.
- Solution:
- We want to know the area of each connected shape in the grid, then take the maximum of these.
- If we are on a land square and explore every square connected to it 4-directionally (and recursively squares connected to those squares, and so on), then the total number of squares explored will be the area of that connected shape.
- To ensure we don't count squares in a shape more than once, let's use seen to keep track of squares we haven't visited before. It will also prevent us from counting the same shape more than once.
- We want to know the area of each connected shape in the grid, then take the maximum of these.
-
class Solution:
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
seen = set()
def area(r, c):
if not (0 <= r < len(grid) and 0 <= c < len(grid[0]) and (r,c) not in seen and grid[r][c]):
return 0
seen.add((r, c))
return (1 + area(r+1, c) + area(r-1, c) + area(r, c-1) + area(r, c+1))
return max(area(r, c) for r in range(len(grid)) for c in range(len(grid[0])))
Day 20
-
792. Number of Matching Subsequences
- Given a string s and an array of strings words, return the number of words[i] that is a subsequence of s
- A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
- Given a string s and an array of strings words, return the number of words[i] that is a subsequence of s
-
Solution 1 (Using Hashmap/Set):
class Solution:
def numMatchingSubseq(self, s: str, words: List[str]) -> int:
matchedWords = []
wordSet = set(words)
for word in wordSet:
matched = 0
for i in range(len(s)):
if matched >= len(word): break
elif s[i] == word[matched]:
matched += 1
if matched == len(word): matchedWords.append(word)
res = 0
for match in matchedWords:
for word in words:
if match == word: res += 1
return res
- Solution 2 (Using @lru_cache memorization technique):
class Solution:
def numMatchingSubseq(self, s: str, words: List[str]) -> int:
result = []
for word in words:
if self.isSubsequence(word, s):
result.append(word)
return len(result)
# Taken from Problem 392 Solution
@lru_cache
def isSubsequence(self, s: str, t: str) -> bool:
if not s:
return True
index = 0
for j in range(len(t)):
if s[index] == t[j]:
index += 1
if index == len(s):
return True
return False
- Solution 3 (Finding char index on the right of cur pointer):
class Solution:
def numMatchingSubseq(self, s: str, words: List[str]) -> int:
def is_sub(s, parent):
cur = 0
for ch in s:
idx = parent.find(ch, cur)
if idx == -1:
return False
cur = idx + 1
return True
cnt = 0
for word in words:
if is_sub(word, s):
cnt += 1
return cnt
Day 21
- 92. Reverse Linked List II
- Given the head of a singly linked list and two integers left and right where left <= right, reverse the nodes of the list from position left to position right, and return the reversed list.
-
- Given the head of a singly linked list and two integers left and right where left <= right, reverse the nodes of the list from position left to position right, and return the reversed list.
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def reverseBetween(self, head: Optional[ListNode], left: int, right: int) -> Optional[ListNode]:
# find the start/left and its prev node
p_prev, p = None, head
for _ in range(left - 1):
p_prev, p = p, p.next
# print(p_prev.val, p.val)
# print("---")
# start reversing
prev, cur = p, p.next
for _ in range(right - left):
# print(cur.next.val, prev.val, cur.val)
cur.next, prev, cur = prev, cur, cur.next
# print("---")
# connecting lefr prev
p.next = cur
if p_prev:
# print(p_prev.next.val, prev.val)
# print(prev.val, head.val)
p_prev.next, prev = prev, head
return prev
Day 22 (Failed to solve at the first time)
- 315. Count of Smaller Numbers After Self
- You are given an integer array nums and you have to return a new counts array. The counts array has the property where counts[i] is the number of smaller elements to the right of nums[i].
# from sortedcontainers import SortedList
class Solution:
def countSmaller(self, nums: List[int]) -> List[int]:
# brute force - TLE
# res = [0 for _ in range(len(nums))]
# for i in range(len(nums)):
# for j in range(i, len(nums)):
# if nums[i] > nums[j]:
# res[i] += 1
# return res
# SortedList with remove, so that the index will be the number of smaller elements to the right of it
# res = []
# sorted_nums = SortedList(nums)
# for e in nums:
# idx = sorted_nums.index(e)
# print(idx)
# print(sorted_nums)
# res.append(idx)
# sorted_nums.remove(e)
# return res
sorted_values, res = [], []
# you cannot declare two distince like this:
# a = b = []; otherwise, they will refer to the same array
# but you can do this with numbers: a = b = 0
for num in nums[::-1]:
# print(sorted_values, res)
idx = bisect.bisect_left(sorted_values, num)
sorted_values.insert(idx, num)
res.append(idx)
return res[::-1]