Understanding the KMP Algorithm
When dealing with text processing and string manipulation, one common problem is the need to find occurrences of a specific pattern within a larger text. The Knuth-Morris-Pratt (KMP) algorithm is a powerful string searching technique that efficiently solves this problem by avoiding unnecessary character comparisons. In this blog, we'll delve into the inner workings of the KMP algorithm and provide you with clear and concise C++ code examples to help you understand and implement it.
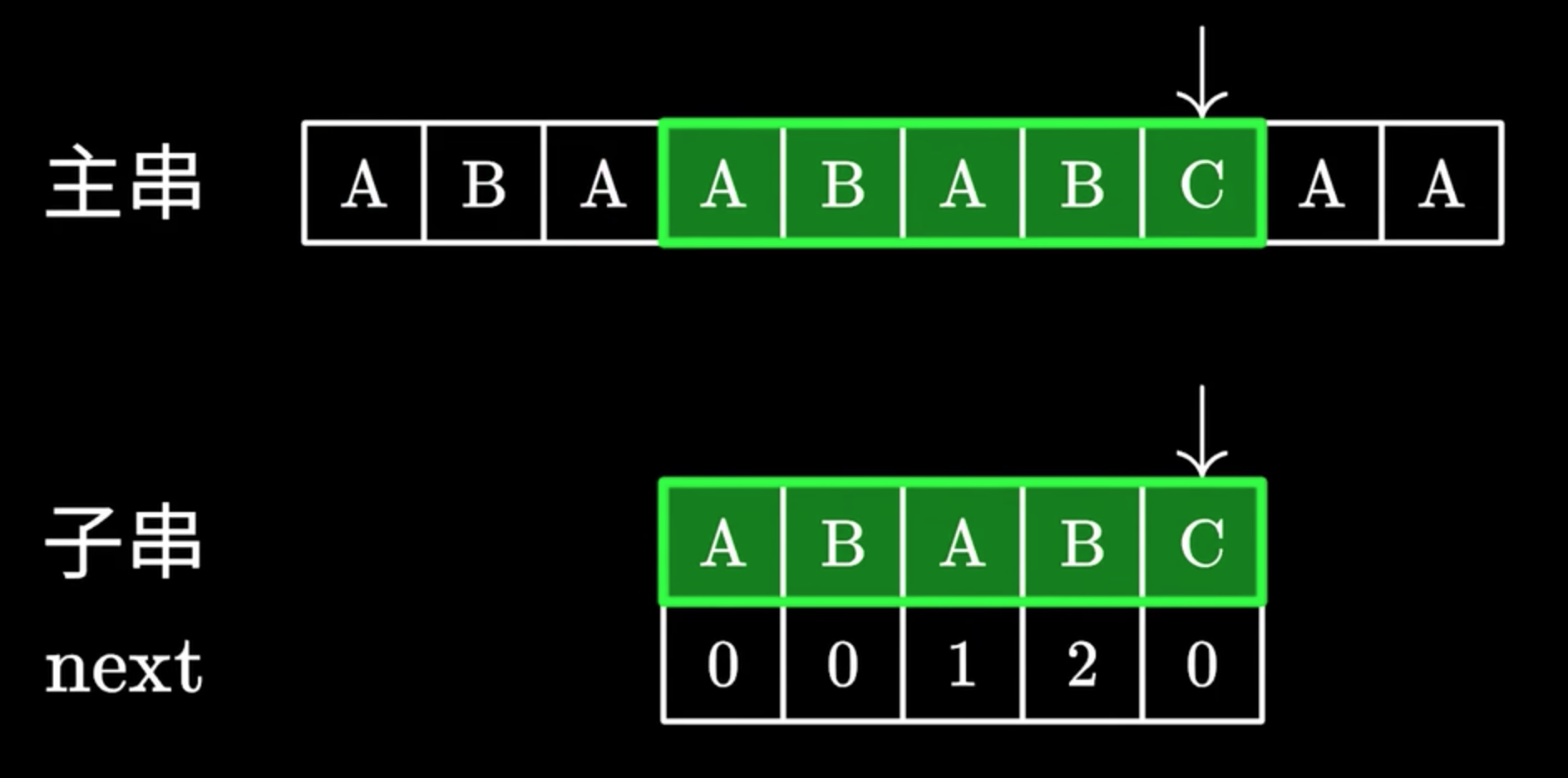
The Problem Statement
Imagine you have a long text string and you want to find all occurrences of a shorter pattern string within the text. The brute-force approach involves sliding the pattern over the text character by character and comparing each character. However, this method becomes inefficient for large texts and patterns.
The KMP Insight
The key insight behind the KMP algorithm is that, during pattern matching, if a mismatch occurs after several matching characters, you don't need to start matching from the beginning of the pattern in the next iteration. The KMP algorithm uses a preprocessing step to build an auxiliary array (LPS - Longest Prefix which is also a Suffix) that stores the length of the proper prefix which is also a proper suffix of the pattern. This array allows the algorithm to skip unnecessary character comparisons when a mismatch occurs.
The Algorithm
Here's the step-by-step breakdown of the KMP algorithm:
- Preprocessing: Create the LPS array for the pattern.
- Matching: Slide the pattern over the text while considering the LPS array.
- If characters match, advance both pointers.
- If a mismatch occurs:
- Use the LPS array to determine how many characters of the pattern to skip.
- Update the pattern pointer accordingly.
- Repeat: Continue until the pattern pointer reaches the end.

Python Implementation
def build_next(p):
"""
Constructing Next/LPS array
"""
next = [0] # first element is 0
prefix_len = 0 # length of the current common prefix/suffix
i = 1
while i < len(p):
if p[prefix_len] == p[i]:
prefix_len += 1
next.append(prefix_len)
i += 1
else:
if prefix_len == 0:
next.append(0)
i += 1
else:
prefix_len = next[prefix_len - 1]
return next
def kmp_search(s, p):
next = build_next(p)
i = 0
j = 0
while i < len(s):
if s[i] == p[j]:
i += 1
j += 1
elif j > 0:
j = next[j - 1]
else:
i += 1
if j == len(p):
return i - j
C++ Implementation
Let's dive into the code. Here's the C++ implementation of the KMP algorithm for LeetCode problem #28:
class Solution {
public:
int strStr(string s, string p) {
// edge case
if (p.empty()) return 0;
int n = s.size(), m = p.size();
s = ' ' + s, p = ' ' + p;
vector<int> next(m + 1);
// constructing next array
for (int i = 2, j = 0; i <= m; i++) {
while (j && p[i] != p[j + 1]) j = next[j];
if (p[i] == p[j + 1]) j++;
next[i] = j;
}
// matching
for (int i = 1, j = 0; i <= n; i++){
while (j && s[i] != p[j + 1]) j = next[j];
if (s[i] == p[j + 1]) j++;
if (j == m) return i - m; // i - m + 1 - 1 -> i - m + 1 is the starting position, -1 for correct indexing
}
return -1;
}
};
Conclusion
The Knuth-Morris-Pratt algorithm is a brilliant approach to solve string matching problems efficiently. By utilizing the LPS array to avoid unnecessary character comparisons, the KMP algorithm significantly improves the performance of pattern matching operations. The provided C++ code examples demonstrate the step-by-step implementation of the algorithm, making it easier to grasp its inner workings. With the KMP algorithm in your toolkit, you're well-equipped to handle text processing challenges effectively and efficiently.